根本的な解決策を生むために必要なのは本質的な問題設定。学生の頃からこの能力を伸ばしていけば、勉強でも仕事でもあらゆる作業のスピードが上がり成果が最大化していく。学習教室「ロジム」代表で、小学校1年生から高校3年生の生徒たちにロジカルシンキングの授業を展開する苅野進氏の特別授業。
※本記事は、苅野進:著『考える力とは、問題をシンプルにすることである。』(ワニブックス刊)より、一部を抜粋編集したものです。
問題文の指示通りでは解けないこともある
次の算数の問題を見てください。
Q:四角形ABCD(下図の黒い部分)の面積を求めなさい。
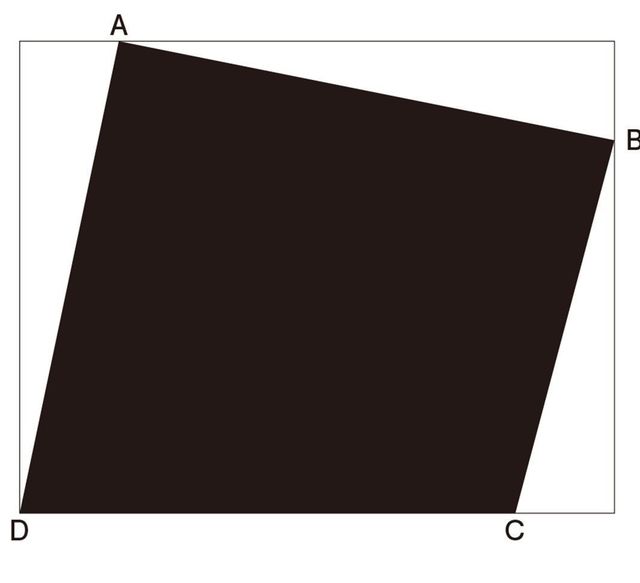
この問題を「四角形ABCDの面積を求める」という問題文の指示通りに「問題設定」をして取り組んでも、解くことができません。
四角形ABCDは正方形や平行四辺形など、求めるための公式があるようなきれいな四角形ではないからです。ここで、問題として設定されている「四角形ABCD」から視点を動かしてみることを考えます。
ある図形の面積は、
- そのものずばりの面積を求める
- より大きな図形から、その図形以外の部分の面積を取り除く
- その図形を分割して求めて、最後に足し合わせる
ことでも、求めることができます。1~3は、同じ目的を達成することができるのです。場合に応じて、どれを問題として設定するかで解けるかどうかが決まります。この問題では前述の通り、1の方針では求めることができそうにありません。
今回は、2の「全体から、四角形ABCD以外の部分の面積を取り除く」という問題設定をすることで、残りの部分として四角形ABCDの面積が求まります。一見不可能そうに見える問題でも、見方を変えて問題を設定し直すことで、突破口が見えてくるという例です。
このように、「目の前の問題は、本当に目的達成のために効果的なのか?」と疑ってみようというのが出発点です。そして、より効果的な問題を設定し直して、結果を出せるようになることが目標です。
宿題には「試験のための勉強」という設定
高校生のとき、全員に一斉に出される宿題をきちんと提出していたのに、いざ試験となるとほとんどできなかった、という経験をお持ちの人は少なくないと思います。期末試験の前に、数学の問題集の指定された範囲を解いたノートを提出するといった類のものです。
先生から与えられた課題(問題)は、「提出日に間に合わせて宿題を提出する」です。これを額面通りに取り組むべき問題として設定してしまう生徒は、提出日に形だけを整えたノートを作成していたはずです。もちろん私もそうでした。
とにかく、すべての問題に取り組む。出来は問われないのだから、適当な式を書いて、赤ペンで直しておけばそれなりの体裁が整います。
こんな作業をしていては、「期日までにノート提出」という問題はクリアできたとしても、「類題が出題されるテストに対応する」という問題が解決できるはずがありません。
「試験のための勉強」という問題設定になっていれば、できなかった問題に印をつけておいて復習したり、重要そうな問題の類題を探したりという、受験のために効果的な作業に取り組んでいたはずです。先生から与えられた問題を表面的に捉えずに、きちんと問題設定できたかどうかが後に大きく響いてくるのです。

